前回は手牌に孤立牌が1枚ある時の牌効率を紹介しました。次は面子完成の一歩手前である、対子(トイツ)そして搭子(ターツ)が手牌にある時の牌効率を見ていきたいと思います。
面子一歩手前、牌2枚の時の牌効率-もくじ
対子(トイツ)と搭子(ターツ)について
まずはおさらいです。対子とは同種・同柄の牌が2枚ある状態のことで、麻雀の基本の和了形である4面子1雀頭の雀頭として使用される他、2翻の役である七対子に使用されます。
![]()
また、ここにさらに同種・同柄の牌が1枚追加されることで面子(刻子)として機能します。
![]()
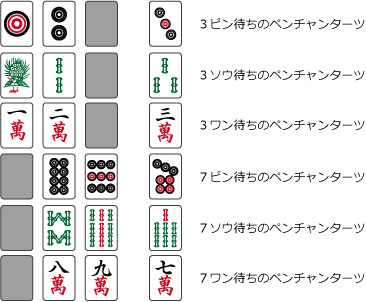
次に搭子についてですが、搭子は連続する3つの数牌(順子)のうちどこか1枚足りない状態のことをいい、不足している部分によって、ペンターツ・リャンメンターツ・カンターツの3種類に分かれます。

どの種類のターツにも有効牌が入ると順子が完成します。
![]()
ちなみに、テンパイ状態でペンターツが残っている待ちをペンチャン待ち、同じくリャンメンターツが残っている待ちをリャンメン待ち、カンターツが残っている待ちをカンチャン待ちといいます。
対子(同種の牌2枚)から考える牌効率
対子が手牌にある時、さらにもう1枚同種の牌が手牌に入れば対子が面子(刻子)に変化します。

対子は和了の基本形である4面子1雀頭の雀頭としても機能しますが、面子は4つも必要なのに対して、必要とされる対子(雀頭)は一つだけ、さらに面子は牌が3枚必要なのに対して、対子(雀頭)はたった2枚で構成されるために、面子と比べると圧倒的に揃いやすく、手牌は面子を優先に揃えていくことになります。
局序盤に対子が刻子に変化する際、「あがる為には対子(雀頭)も必要だから、この3枚目はいらない!!」なんて考えて切り捨てないようにしましょう。
| 手牌 | 受け入れ牌 | 合計枚数 |
|---|---|---|
| 風牌 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 三元牌 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 数牌 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
| 計2枚 | ||
このように、字牌であろうと数牌であろうと受け入れ牌はそれぞれ2枚となります。受け入れ枚数自体は変わりませんが、対子を崩して残った牌は牌の種類によって受け入れ枚数が変わってきます。同じ対子を崩すなら、以下の順で対子を崩すようにします。
| 牌効率から見る孤立牌切り捨て順 | ||
|---|---|---|
| 手牌 | 受け入れ枚数 | 切り捨て順 |
| 各3枚 | 捨てる | |
| 各11枚 | ↓ | |
| 各15枚 | ↓ | |
| 各19枚 | 残す | |
特に、字牌の対子は面子にしようとする場合、同種の牌の3枚目を引き当て刻子にするしかありませんが、数牌はペンターツやカンターツ・リャンメンターツへの変化が期待できます。そのため同じ対子であっても、字牌の対子と数牌の対子を比べると数牌の対子が優位となります。
孤立牌の受け入れ枚数は牌効率の考え方で詳しく紹介しているので、そちらを参考にしてみてください。
ペンターツ(12・89)から考える牌効率
ペンターツは1種の数牌に対して、12・89と必ず2つ存在します。数牌は3種類なので、ペンターツは全部で6種類といくとになりますね。
受け入れ牌は以下の通りです。
| 手牌 | 受け入れ牌 | 合計枚数 |
|---|---|---|
| 計4枚 | ||
| 計4枚 |
対子の受け入れ牌2枚と比べるとペンターツの受け入れ牌は4枚ありますが、それでも良い形とは言えませんね。
カンターツ(7種)から考える牌効率
カンターツは、順子の真ん中の数牌が抜け落ちたターツでしたね。このカンターツは1種類の数牌に付き7つあり、数牌は3種(ワンズ・ピンズ・ソウズ)あるので、合計21種あることになりますね。受け入れ牌の枚数は以下の通りです。
| 手牌 | 受け入れ牌 | 合計枚数 |
|---|---|---|
| 計4枚 | ||
| 計4枚 | ||
| 計4枚 | ||
| 計4枚 | ||
| 計4枚 | ||
| 計4枚 | ||
| 計4枚 |
どのカンターツも受け入れは4枚となりペンターツと同じとなります。ただしカンターツはペンターツとは違い、リャンメンターツへの変化が期待できます。
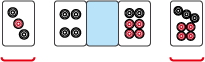
どういう事かというと、ペンターツをリャンメンターツに変化させようと思うと、下の牌姿のようにペンターツとは関係のない連続するチュンチャンパイを都合よく2枚引いてこないといけません。これは変化というより、全く別の搭子をつくることになりますね。

一方カンターツは、該当する数牌を1枚引いてくるだけでリャンメンターツへの変化が期待できます。つまり、受け入れ枚数が同じペンターツとカンターツでもリャンメンターツへの変化が期待できる、カンターツの方が優位ということがわかります。
リャンメンターツ(6種)から考える牌効率
複合待ちを除けば受け入れ牌が8枚もある最も良形といえるターツがこのリャンメンターツとなります。リャンメンターツは数牌1種につき6つあり、数牌は3種(ワンズ・ピンズ・ソウズ)あるので、合計18種あることになります。受け入れ牌のパターンは以下の通りとなります。
| 手牌 | 受け入れ牌 | 合計枚数 |
|---|---|---|
| 計8枚 | ||
| 計8枚 | ||
| 計8枚 | ||
| 計8枚 | ||
| 計8枚 | ||
| 計8枚 |
面子一歩手前、牌2枚の時の牌効率-まとめ
あと一枚有効牌が入れば面子が完成する対子や搭子。似たような2枚構成の牌姿ですが受け入れ牌や優位性が違うことがわかると思います。まとめると以下のようになります。
| 手牌 | 受け入れ枚数 | 優位性 |
|---|---|---|
| リャンメンターツ |
8枚 | 高い |
| カンターツ |
4枚 | ↓ |
| ペンターツ |
4枚 | ↓ |
| 数牌の対子 |
2枚 | ↓ |
| 字牌の対子 |
2枚 | 低い |

